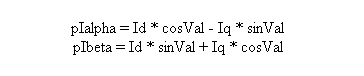|
| static __INLINE void | arm_inv_park_f32 (float32_t Id, float32_t Iq, float32_t *pIalpha, float32_t *pIbeta, float32_t sinVal, float32_t cosVal) |
| | Floating-point Inverse Park transform.
|
| |
| static __INLINE void | arm_inv_park_q31 (q31_t Id, q31_t Iq, q31_t *pIalpha, q31_t *pIbeta, q31_t sinVal, q31_t cosVal) |
| | Inverse Park transform for Q31 version.
|
| |
Inverse Park transform converts the input flux and torque components to two-coordinate vector.
The function operates on a single sample of data and each call to the function returns the processed output. The library provides separate functions for Q31 and floating-point data types.
- Algorithm
-
where
pIalpha and pIbeta are the stator vector components, Id and Iq are rotor vector components and cosVal and sinVal are the cosine and sine values of theta (rotor flux position).
- Fixed-Point Behavior
- Care must be taken when using the Q31 version of the Park transform. In particular, the overflow and saturation behavior of the accumulator used must be considered. Refer to the function specific documentation below for usage guidelines.
- Parameters
-
| [in] | Id | input coordinate of rotor reference frame d |
| [in] | Iq | input coordinate of rotor reference frame q |
| [out] | pIalpha | points to output two-phase orthogonal vector axis alpha |
| [out] | pIbeta | points to output two-phase orthogonal vector axis beta |
| [in] | sinVal | sine value of rotation angle theta |
| [in] | cosVal | cosine value of rotation angle theta |
- Parameters
-
| [in] | Id | input coordinate of rotor reference frame d |
| [in] | Iq | input coordinate of rotor reference frame q |
| [out] | pIalpha | points to output two-phase orthogonal vector axis alpha |
| [out] | pIbeta | points to output two-phase orthogonal vector axis beta |
| [in] | sinVal | sine value of rotation angle theta |
| [in] | cosVal | cosine value of rotation angle theta |
Scaling and Overflow Behavior:
- The function is implemented using an internal 32-bit accumulator. The accumulator maintains 1.31 format by truncating lower 31 bits of the intermediate multiplication in 2.62 format. There is saturation on the addition, hence there is no risk of overflow.