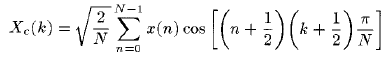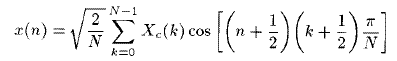|
| void | arm_dct4_f32 (const arm_dct4_instance_f32 *S, float32_t *pState, float32_t *pInlineBuffer) |
| | Processing function for the floating-point DCT4/IDCT4.
|
| |
| arm_status | arm_dct4_init_f32 (arm_dct4_instance_f32 *S, arm_rfft_instance_f32 *S_RFFT, arm_cfft_radix4_instance_f32 *S_CFFT, uint16_t N, uint16_t Nby2, float32_t normalize) |
| | Initialization function for the floating-point DCT4/IDCT4.
|
| |
| arm_status | arm_dct4_init_q15 (arm_dct4_instance_q15 *S, arm_rfft_instance_q15 *S_RFFT, arm_cfft_radix4_instance_q15 *S_CFFT, uint16_t N, uint16_t Nby2, q15_t normalize) |
| | Initialization function for the Q15 DCT4/IDCT4.
|
| |
| arm_status | arm_dct4_init_q31 (arm_dct4_instance_q31 *S, arm_rfft_instance_q31 *S_RFFT, arm_cfft_radix4_instance_q31 *S_CFFT, uint16_t N, uint16_t Nby2, q31_t normalize) |
| | Initialization function for the Q31 DCT4/IDCT4.
|
| |
| void | arm_dct4_q15 (const arm_dct4_instance_q15 *S, q15_t *pState, q15_t *pInlineBuffer) |
| | Processing function for the Q15 DCT4/IDCT4.
|
| |
| void | arm_dct4_q31 (const arm_dct4_instance_q31 *S, q31_t *pState, q31_t *pInlineBuffer) |
| | Processing function for the Q31 DCT4/IDCT4.
|
| |
Representation of signals by minimum number of values is important for storage and transmission. The possibility of large discontinuity between the beginning and end of a period of a signal in DFT can be avoided by extending the signal so that it is even-symmetric. Discrete Cosine Transform (DCT) is constructed such that its energy is heavily concentrated in the lower part of the spectrum and is very widely used in signal and image coding applications. The family of DCTs (DCT type- 1,2,3,4) is the outcome of different combinations of homogeneous boundary conditions. DCT has an excellent energy-packing capability, hence has many applications and in data compression in particular.
DCT is essentially the Discrete Fourier Transform(DFT) of an even-extended real signal. Reordering of the input data makes the computation of DCT just a problem of computing the DFT of a real signal with a few additional operations. This approach provides regular, simple, and very efficient DCT algorithms for practical hardware and software implementations.
DCT type-II can be implemented using Fast fourier transform (FFT) internally, as the transform is applied on real values, Real FFT can be used. DCT4 is implemented using DCT2 as their implementations are similar except with some added pre-processing and post-processing. DCT2 implementation can be described in the following steps:
- Re-ordering input
- Calculating Real FFT
- Multiplication of weights and Real FFT output and getting real part from the product.
This process is explained by the block diagram below:

Discrete Cosine Transform - type-IV
- Algorithm:
- The N-point type-IV DCT is defined as a real, linear transformation by the formula:
where
k = 0,1,2,.....N-1
- Its inverse is defined as follows:
where
n = 0,1,2,.....N-1
- The DCT4 matrices become involutory (i.e. they are self-inverse) by multiplying with an overall scale factor of sqrt(2/N). The symmetry of the transform matrix indicates that the fast algorithms for the forward and inverse transform computation are identical. Note that the implementation of Inverse DCT4 and DCT4 is same, hence same process function can be used for both.
- Lengths supported by the transform:
- As DCT4 internally uses Real FFT, it supports all the lengths supported by arm_rfft_f32(). The library provides separate functions for Q15, Q31, and floating-point data types.
- Instance Structure
- The instances for Real FFT and FFT, cosine values table and twiddle factor table are stored in an instance data structure. A separate instance structure must be defined for each transform. There are separate instance structure declarations for each of the 3 supported data types.
- Initialization Functions
- There is also an associated initialization function for each data type. The initialization function performs the following operations:
- Sets the values of the internal structure fields.
- Initializes Real FFT as its process function is used internally in DCT4, by calling arm_rfft_init_f32().
- Use of the initialization function is optional. However, if the initialization function is used, then the instance structure cannot be placed into a const data section. To place an instance structure into a const data section, the instance structure must be manually initialized. Manually initialize the instance structure as follows:
*arm_dct4_instance_f32 S = {N, Nby2, normalize, pTwiddle, pCosFactor, pRfft, pCfft};
*arm_dct4_instance_q31 S = {N, Nby2, normalize, pTwiddle, pCosFactor, pRfft, pCfft};
*arm_dct4_instance_q15 S = {N, Nby2, normalize, pTwiddle, pCosFactor, pRfft, pCfft};
where N is the length of the DCT4; Nby2 is half of the length of the DCT4; normalize is normalizing factor used and is equal to sqrt(2/N); pTwiddle points to the twiddle factor table; pCosFactor points to the cosFactor table; pRfft points to the real FFT instance; pCfft points to the complex FFT instance; The CFFT and RFFT structures also needs to be initialized, refer to arm_cfft_radix4_f32() and arm_rfft_f32() respectively for details regarding static initialization.
- Fixed-Point Behavior
- Care must be taken when using the fixed-point versions of the DCT4 transform functions. In particular, the overflow and saturation behavior of the accumulator used in each function must be considered. Refer to the function specific documentation below for usage guidelines.
- Parameters
-
| [in,out] | *S | points to an instance of floating-point DCT4/IDCT4 structure. |
| [in] | *S_RFFT | points to an instance of floating-point RFFT/RIFFT structure. |
| [in] | *S_CFFT | points to an instance of floating-point CFFT/CIFFT structure. |
| [in] | N | length of the DCT4. |
| [in] | Nby2 | half of the length of the DCT4. |
| [in] | normalize | normalizing factor. |
- Returns
- arm_status function returns ARM_MATH_SUCCESS if initialization is successful or ARM_MATH_ARGUMENT_ERROR if
fftLenReal is not a supported transform length.
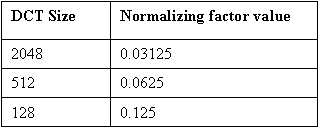
- Normalizing factor:
- The normalizing factor is
sqrt(2/N), which depends on the size of transform N. Floating-point normalizing factors are mentioned in the table below for different DCT sizes:
References ARM_MATH_ARGUMENT_ERROR, ARM_MATH_SUCCESS, arm_rfft_init_f32(), cos_factors_128, cos_factors_2048, cos_factors_512, cos_factors_8192, arm_dct4_instance_f32::N, arm_dct4_instance_f32::Nby2, arm_dct4_instance_f32::normalize, arm_dct4_instance_f32::pCfft, arm_dct4_instance_f32::pCosFactor, arm_dct4_instance_f32::pRfft, arm_dct4_instance_f32::pTwiddle, status, Weights_128, Weights_2048, Weights_512, and Weights_8192.
- Parameters
-
| [in,out] | *S | points to an instance of Q15 DCT4/IDCT4 structure. |
| [in] | *S_RFFT | points to an instance of Q15 RFFT/RIFFT structure. |
| [in] | *S_CFFT | points to an instance of Q15 CFFT/CIFFT structure. |
| [in] | N | length of the DCT4. |
| [in] | Nby2 | half of the length of the DCT4. |
| [in] | normalize | normalizing factor. |
- Returns
- arm_status function returns ARM_MATH_SUCCESS if initialization is successful or ARM_MATH_ARGUMENT_ERROR if
N is not a supported transform length.
- Normalizing factor:
- The normalizing factor is
sqrt(2/N), which depends on the size of transform N. Normalizing factors in 1.15 format are mentioned in the table below for different DCT sizes:
References ARM_MATH_ARGUMENT_ERROR, ARM_MATH_SUCCESS, arm_rfft_init_q15(), cos_factorsQ15_128, cos_factorsQ15_2048, cos_factorsQ15_512, cos_factorsQ15_8192, arm_dct4_instance_q15::N, arm_dct4_instance_q15::Nby2, arm_dct4_instance_q15::normalize, arm_dct4_instance_q15::pCfft, arm_dct4_instance_q15::pCosFactor, arm_dct4_instance_q15::pRfft, arm_dct4_instance_q15::pTwiddle, status, WeightsQ15_128, WeightsQ15_2048, WeightsQ15_512, and WeightsQ15_8192.
- Parameters
-
| [in,out] | *S | points to an instance of Q31 DCT4/IDCT4 structure. |
| [in] | *S_RFFT | points to an instance of Q31 RFFT/RIFFT structure |
| [in] | *S_CFFT | points to an instance of Q31 CFFT/CIFFT structure |
| [in] | N | length of the DCT4. |
| [in] | Nby2 | half of the length of the DCT4. |
| [in] | normalize | normalizing factor. |
- Returns
- arm_status function returns ARM_MATH_SUCCESS if initialization is successful or ARM_MATH_ARGUMENT_ERROR if
N is not a supported transform length.
- Normalizing factor:
- The normalizing factor is
sqrt(2/N), which depends on the size of transform N. Normalizing factors in 1.31 format are mentioned in the table below for different DCT sizes:
References ARM_MATH_ARGUMENT_ERROR, ARM_MATH_SUCCESS, arm_rfft_init_q31(), cos_factorsQ31_128, cos_factorsQ31_2048, cos_factorsQ31_512, cos_factorsQ31_8192, arm_dct4_instance_q31::N, arm_dct4_instance_q31::Nby2, arm_dct4_instance_q31::normalize, arm_dct4_instance_q31::pCfft, arm_dct4_instance_q31::pCosFactor, arm_dct4_instance_q31::pRfft, arm_dct4_instance_q31::pTwiddle, status, WeightsQ31_128, WeightsQ31_2048, WeightsQ31_512, and WeightsQ31_8192.
- Parameters
-
| [in] | *S | points to an instance of the Q31 DCT4 structure. |
| [in] | *pState | points to state buffer. |
| [in,out] | *pInlineBuffer | points to the in-place input and output buffer. |
- Returns
- none.
- Input an output formats:
- Input samples need to be downscaled by 1 bit to avoid saturations in the Q31 DCT process, as the conversion from DCT2 to DCT4 involves one subtraction. Internally inputs are downscaled in the RFFT process function to avoid overflows. Number of bits downscaled, depends on the size of the transform. The input and output formats for different DCT sizes and number of bits to upscale are mentioned in the table below:
References arm_cmplx_mult_cmplx_q31(), arm_mult_q31(), arm_rfft_q31(), arm_shift_q31(), arm_dct4_instance_q31::N, arm_dct4_instance_q31::Nby2, arm_dct4_instance_q31::normalize, arm_dct4_instance_q31::pCosFactor, arm_dct4_instance_q31::pRfft, and arm_dct4_instance_q31::pTwiddle.
- cosFactor tables are generated using the formula :
cos_factors[n] = 2 * cos((2n+1)*pi/(4*N))
- C command to generate the table
for(i = 0; i< N; i++)
{
cos_factors[i]= 2 * cos((2*i+1)*c/2);
}
- where
N is the number of factors to generate and c is pi/(2*N)
Referenced by arm_dct4_init_f32().
- cosFactor tables are generated using the formula :
cos_factors[n] = 2 * cos((2n+1)*pi/(4*N))
- C command to generate the table
for(i = 0; i< N; i++)
{
cos_factors[i]= 2 * cos((2*i+1)*c/2);
}
- where
N is the number of factors to generate and c is pi/(2*N)
- Then converted to q15 format by multiplying with 2^31 and saturated if required.
Referenced by arm_dct4_init_q15().
| const q31_t cos_factorsQ31_128[128] |
|
static |
- cosFactor tables are generated using the formula :
cos_factors[n] = 2 * cos((2n+1)*pi/(4*N))
- C command to generate the table
for(i = 0; i< N; i++)
{
cos_factors[i]= 2 * cos((2*i+1)*c/2);
}
- where
N is the number of factors to generate and c is pi/(2*N)
- Then converted to q31 format by multiplying with 2^31 and saturated if required.
Referenced by arm_dct4_init_q31().
| const q31_t cos_factorsQ31_2048[2048] |
|
static |
| const q31_t cos_factorsQ31_512[512] |
|
static |
| const q31_t cos_factorsQ31_8192[8192] |
|
static |
- Weights tables are generated using the formula :
weights[n] = e^(-j*n*pi/(2*N))
- C command to generate the table
for(i = 0; i< N; i++)
{
weights[2*i]= cos(i*c);
weights[(2*i)+1]= -sin(i * c);
}
- Where
N is the Number of weights to be calculated and c is pi/(2*N)
- In the tables below the real and imaginary values are placed alternatively, hence the array length is
2*N.
Referenced by arm_dct4_init_f32().
- Weights tables are generated using the formula :
weights[n] = e^(-j*n*pi/(2*N))
- C command to generate the table
for(i = 0; i< N; i++)
{
weights[2*i]= cos(i*c);
weights[(2*i)+1]= -sin(i * c);
}
- where
N is the Number of weights to be calculated and c is pi/(2*N)
- Converted the output to q15 format by multiplying with 2^31 and saturated if required.
- In the tables below the real and imaginary values are placed alternatively, hence the array length is
2*N.
Referenced by arm_dct4_init_q15().
| const q31_t WeightsQ31_128[256] |
|
static |
- Weights tables are generated using the formula :
weights[n] = e^(-j*n*pi/(2*N))
- C command to generate the table
for(i = 0; i< N; i++)
{
weights[2*i]= cos(i*c);
weights[(2*i)+1]= -sin(i * c);
}
- where
N is the Number of weights to be calculated and c is pi/(2*N)
- Convert the output to q31 format by multiplying with 2^31 and saturated if required.
- In the tables below the real and imaginary values are placed alternatively, hence the array length is
2*N.
Referenced by arm_dct4_init_q31().
| const q31_t WeightsQ31_2048[4096] |
|
static |
| const q31_t WeightsQ31_512[1024] |
|
static |
| const q31_t WeightsQ31_8192[16384] |
|
static |